
#Two way anova spss code how to#
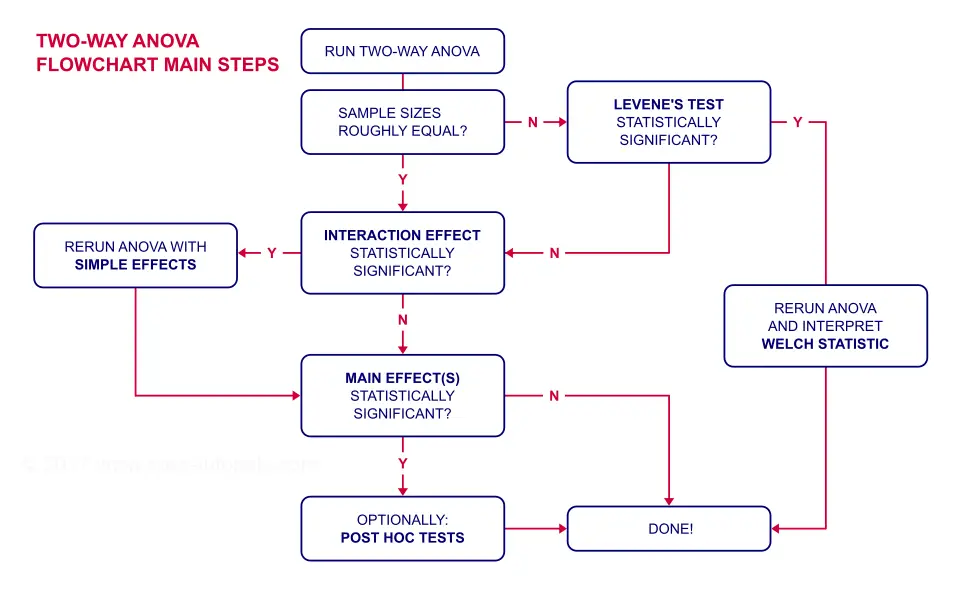
So let’s look at how to handle each of those in the two packages.įrankly, I hate these and wish people would stop doing them. I note that the last of those is probably the best approach but they should be aware of the others because they’ll see them in print and they should know how to do them. The three ways are doing posthocs on cells, doing simple main effects, and doing interaction contrasts. I teach them three ways to deal with interactions, though I don’t actually recommend they use one of them. So, what to do with these results? Well, I always instruct my students that they should deal with the interaction first, before even looking at the main effects. So, a slight edge to SPSS on effect size.

On the other hand, because the table produced is a first-class object in R, it is possible to write a function that would compute relevant effect size metrics-but why should I have to do this? Why is this not even an option in R, when most journals (at least in psychology) now encourage or flat-out require reporting of effect size? It sure would be nice if the ANOVA table included the total sum of squares, though, as that would save some steps in the computation.

R doesn’t automatically give us the partial eta squared values, but the ANOVA table has everything needed on it to compute them. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Īgain, there’s annoying whitespace in the tops of the R plots, but otherwise they’re no better or worse than the SPSS plots. GroupF = factor(Group, labels=c("ATCs", "Students"))
#Two way anova spss code code#
The code looks like this:ĬlutterF = factor(Clutter, labels=c("High", "Medium", "Low")) First we’ll create and label factors (assuming the data set is attached). It doesn’t produce interaction plots, but those are pretty easy to get. The most straightforward is just to use the “aov()” function for generating an ANOVA. As usual, there are a whole lot of different ways to get a simple ANOVA out of R. The interaction plots are sort of stupid in that SPSS always zooms in the maximum amount to exaggerate differences, and the color choices aren’t great, but it’s not awful. We get a nice table of factors, a very complete ANOVA table and two interaction plots that look like these:įor those that dislike partial eta squared as a measure of effect size (I’m not a huge fan myself), SPSS nicely reports all the relevant quantities so that calculation of eta-squared or omega-squared is pretty straightforward. First, though, we’ll label the levels of the variables, then run the ANOVA, like this:ĪDD VALUE LABELS Group 0 "ATCs" 1 "Students".ĪDD VALUE LABELS Clutter 0 "High" 1 "Medium" 2 "Low". The SPSS code for generating the basic two-way ANOVA and generating interaction plots is pretty simple. I’m not going to go into things like descriptives and box plots because the data set is clean and I’ve already covered that stuff in previous posts. There is one dependent variable, “Targets” (number of targets detected by each subject), “Group” with two levels, air traffic controllers (ATCs) and regular college sophomores, and “Clutter” indexing the amount of clutter on the display with three levels: high, medium, and low. (A 2 x 2 doesn’t give much opportunity to do contrasts, which is why I don’t start there.) The data set we start with is this one: detection.xls. I start my students with almost, but not quite, the simplest two-way ANOVA possible, a 2 x 3.
The world gets much more complicated when things are not balanced and SPSS and R do not agree in how they handle that, so that situation will get its own post. Today’s topic is factorial between-subjects ANOVA, but with a particular constraint: the design discussed here will be balanced (or orthogonal) in that the number of subjects in each cell will be the same. Type III Sum of Squares Python code: formula = 'dependent_variable ~ C(factor_1) * C(factor_2)'Īlso R2 = 0.722, and adj R2 = 0.694 for the above ANOVAs.Sorry for the lag between posts, but the semester’s been busy and I’ve been sick. Model = ols(formula, data=df_freq_time).fit()
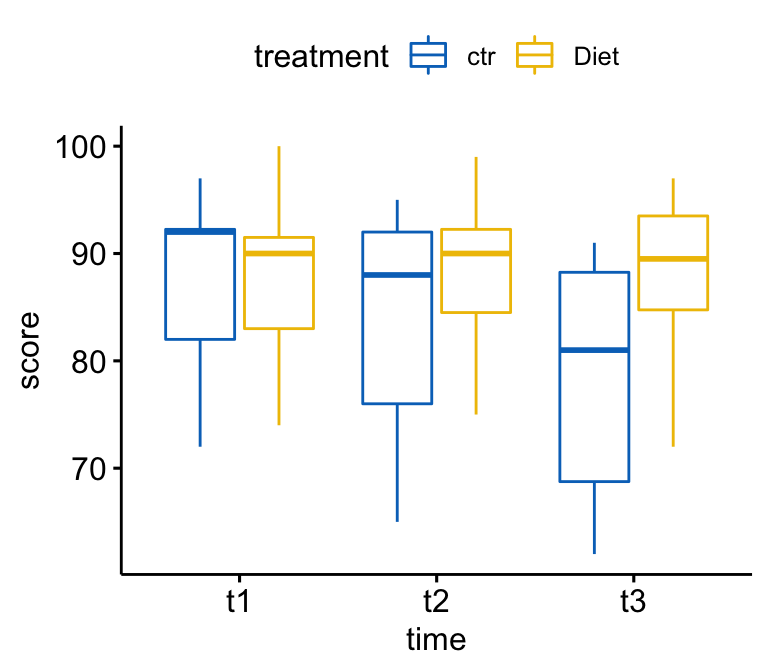
Type II Sum of Squares Python code: formula = 'dependent_variable ~ C(factor_1) * C(factor_2)' My reputation is also too low to comment on that question. My question is very similar to this one, which was unanswered. Why do they disagree? And why is the typ=3 the most different? Moreover, although SPSS and Graphpad calculate Type III Sum of Squares, the statsmodel ANOVA output when typ=3 is the most aberrant, whereas typ=1 or 2 are much closer. Comparing the outputs you can see that the SS_Factor_1 values, and the Adjusted R2 are different for Python vs SPSS/Graphpad. I am learning to use Python for my statistical analyses, and while figuring out how to perform a 2-way ANOVA with statsmodels I found that my Python code yielded slightly aberrant values.


 0 kommentar(er)
0 kommentar(er)
